OMPディレクティブを​使った​並列処理​（OpenMP）…​その​②

前回記事に続き、少し詳細な制御を説明します。…詳細と言ってもほんの少しだけです。

１. private補助構文

• 以下記載例のループ変数 j が、各スレッドで別の変数を確保して実行される。
  例えばワーカスレッド1～4があるのならj1～j4の変数がそれぞれのスレッドで確保されて実行されます。
• private( j ) がない場合、各スレッドで 共有変数 j のカウントを独立して行ってしまい、逐次実行の場合と結果が異なる。

#pragma omp parallel for private( j )
for (i=0; i<100; i++) {
    for (j=0; j<100; j++) {
        a[ i ] = a[ i ] + amat[ i ][ j ]* b[ j ];
    }
}

並列処理の意味を考えるとそもそもデフォルトprivateじゃないの？とか思うのですが違うようです……ここら辺がOpenMP構文の取っ付き難いところかもしれませんね。
並列処理の実行イメージが頭に浮かばないと期待した結果通りの処理が組めません。
ちなみに前回記事で説明したreduction構文の場合はデフォルトprivateになります。
(以下コード例のsum部分)。これはまぁそれはそうかという感じですね。

#pragma omp parallel for reduction (+:sum)
for (i = 1; i < 定数; i++) {
    sum += a[i] * b[i];
}
例えばワーカスレッド1～4に対してsum1～sum4がそれぞれ確保されて別々に計算される。  
最終結果をsumにまとめる。

2. schedule補助構文

Parallel for構文では、対象ループの範囲（例えば１～ｎの長さ）を、単純にスレッド個数分に分割（連続するように分割）して、並列処理をする。
この場合、各スレッドの処理負荷に偏りがあると並列処理のメリットが失われることがある。
以下の処理イメージを見ればわかりやすいかと思います。

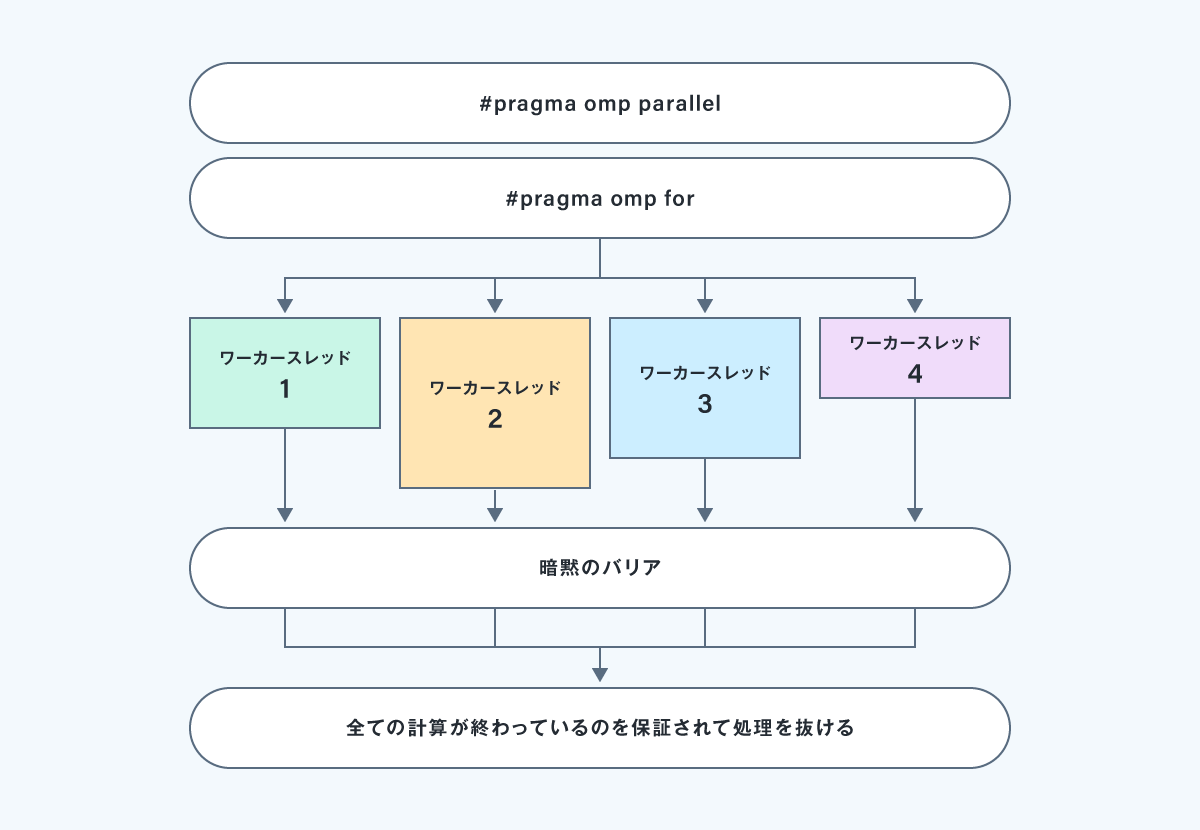
この事例ではワーカスレッド4が早く終わりすぎる、かつ暗黙のバリア地点で他のスレッドがワーカスレッド2が終わるのを待つ形になります。
これでは、せっかくの並列処理なのに充分な効果を出すことができません。

for文の単純ループ処理などでそんな極端な処理時間の差が出ることがあるの？と思われるかもしれませんが、あります！  
単純な除算処理であっても以下のように処理速度のばらつきがあります。  
具体的には割り算処理だと２のべき乗の演算が続くと、思いのほか早く終わってしまう処理も存在するのです。  
- Integer division:整数除算 15-40クロック消費  
- 128-bit vector division:128ビットベクター除算(32ビット4段で並列除算する) 10-70クロック消費  
- Floating-point division:実数除算 25-70クロック消費  

この負荷の偏りを解決するにはループの割り当て間隔を短くし、そして各ワーカスレッドに循環するように処理を割り当てます。
「割り当ての間隔＝チャンクサイズ」の最適な値はハードウェアと対象となる処理に依存します。

以下チャンクサイズ割り当てのdynamic補助構文です。  

#pragma omp parallel for private( j ) schedule(dynamic,10)
for (i=0; i<N1; i++) {
    for ( j=0; j<N2; j++) {
        …
    }
}

N1のループを0～9, 10～19, …という形で分割してワーカスレッド1、スレッド2、…とワーカスレッドが空いている順に各ループ処理を割り当てる。  
★ dynamic,10(チャンクサイズ)はチューニングによって最適な値を決める(以降の構文でも同様)。  
dynamic補助構文では、処理が終了したスレッドから早い者勝ちで次のループ処理が割り当てられます。  

続いてstatic補助構文です。
#pragma omp parallel for private( j ) schedule(static,10)
for (i=0; i<N1; i++) {

…あとは同じ
static補助構文ではワーカスレッド1から順番に１、２、３、４、１、２、３…というように、ラウンドロビン式に循環するように割り当てます。
上記の例だとN1÷10でループが分割されワーカスレッドが順番に処理を実行していきます。
実行の順番がコンパイル時に確定して変わらなく、処理が分割される数も同様にコンパイル時に予め決まります。

続いてguided補助構文です。
#pragma omp parallel for private( j ) schedule(guided,10)
for (i=0; i<N1; i++) {

…あとは同じ
guided補助構文ではループ長をチャンクサイズで分割して、徐々にチャンクサイズを小さくしながら処理が終了したスレッドから早い者勝ちで処理を割り当てます。
1．チャンクサイズの指定が１の場合、残りの反復処理をスレッド数で割ったおおよその値が各チャンクのサイズになる。
2. チャンクサイズは １ に向かって指数的に小さくなる。
3. チャンクサイズに １より大きい k を指定した場合、チャンク サイズは指数的に k まで小さくなるが、最後のチャンクは k より小さくなる場合がある。
4. チャンクサイズが指定されていない場合、デフォルトは １ になる。
処理イメージ図を以下に示します。

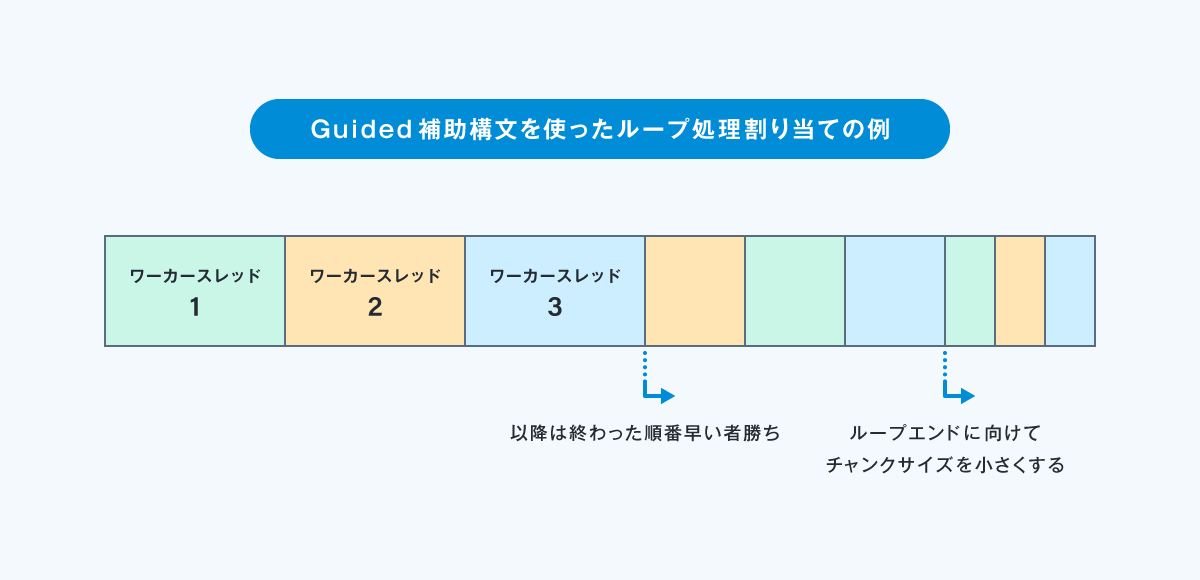
続いて上記の３つの補助構文(dynamic、guided、static)の使いどころの説明になります。

① dynamic、guided補助構文の使いどころ

forループ処理負荷の偏りが、実際に処理を実行してみないと判らない場合に採用します。
チャンクサイズの最適化のために、事前にチューニングコスト(チャンクサイズを変えながら何度も試行する)を掛けることにより、より最適化された処理を組むことができます。

② static補助構文の使いどころ

dynamic/guidedなどの実行時スケジューリングは、仕組み上システムのオーバーヘッドが入りますが、staticはオーバーヘッドがほとんどありません。
そのため事前に負荷が平均的に分散されるループ範囲を調べたうえでチャンクサイズを指定してstaticスケジューリングを使うと、最も効率が良い処理となる可能性があります。

3. Critical補助構文

直後の一文またはブロックの実行を１つのスレッドに制限します。
このような領域をクリティカル領域と呼びます。
以下記述例のnameはクリティカル領域の識別に使用します。
皆様お気付きの通り、通常のマルチスレッドプログラミングでいうところの排他制御の役割を果たします。
クリティカル領域の安易な使用は並列処理のメリットを失わせ、パフォーマンスへの影響が大きくなることがあるので注意しましょう。

#pragma omp critical (name)
 {
    …
 } 

4. Atomic補助構文

直後の一行をアトミック命令(分離不可能な命令＝複数スレッドが実行衝突せずに安全に共有変数の値を更新する)として実行します。 指定できるのは１行のみでcritical補助構文のようにブロック指定ができません。

#pragma omp atomic
i++;

「#pragma omp critical」は「#pragma omp atomic」の上位互換のイメージですね。
しかし、「#pragma omp atomic」指示文を用いると一般にハードウェア命令による値の更新を行うため「#pragma omp critical」指示文を使うよりも処理速度が速くなります。
特に必要が無ければ(複数行で表現する必要が無ければ)atomic構文を使うようにしましょう。

今回は以上になります。
個人的にはOpenMPを使った並列処理というのは、あまり複雑なマルチスレッドプログラミングには向かなくてシンプルな処理記述で並列処理の効果を上げるように作られていると見えていて、前回記事と今回記事の記載内容を抑えていれば充分かなと考えています。
まずは自作TOOLなどで効果を実感して、感覚を掴んでおきましょう。
仕組みが判れば恐れるに足らずです。
逆に仕組みが判っていないと逐次実行した場合とは処理結果が変わったりとよく判らない動きをすると思います。

長文にお付き合いいただきありがとうございました。