はじめに
3Dグラフィックス基礎シリーズ第2弾となります。
第1回の記事はこちら
第2回目のテーマは「ポリゴンと頂点インデックス」です。
第1回目で、3D空間上での座標指定(頂点)について簡単に説明しました。
今回は、複数の頂点から実際に図形として成立させるための3Dグラフィックスの手順について説明していきます。
前回のおさらい
前回、3D空間上で立方体を登場させるためには、以下の通り3D空間上に8個の頂点(①~⑧)を指定する必要があると説明しました。
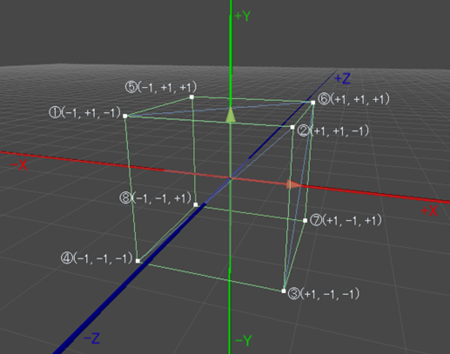
Unityエディタのスクリーンショット画像
ポリゴン
3Dグラフィックスの世界では、3個の頂点で構成された面のことを「ポリゴン」と言います。 例えば、以下の図の通り、頂点①②③で囲まれた領域で形成される三角形がポリゴンとなります。 3Dグラフィックスでは、基本的にこのポリゴン単位で描画が行われていきます。
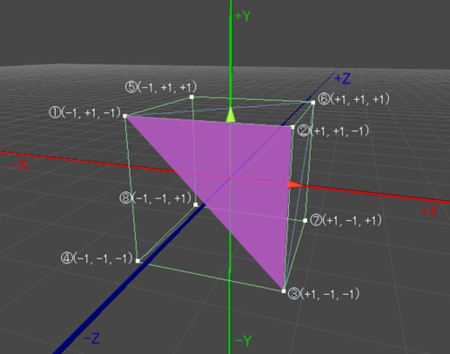
Unityエディタのスクリーンショット画像
そして、「どの頂点を繋げてポリゴンを形成するか」という情報を頂点インデックスと言います。
すなわち、上記立方体を描画したい場合、一番手前の面については、頂点インデックスに以下の2つの組み合わせを持たせれば、三角形ポリゴンが2つ作られて、1つの四角形(正方形)が表現できます。
- 頂点インデックスの組み合わせ1 : 頂点①②③ = ポリゴン1
- 頂点インデックスの組み合わせ2 : 頂点①③④ = ポリゴン2
上記の2つの三角形ポリゴンを組み合わせることで正方形の平面を表現すると以下の図のようになります。
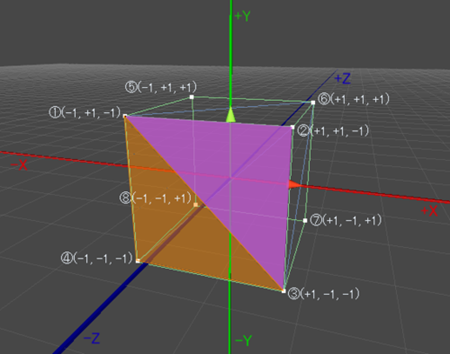
Unityエディタのスクリーンショット画像
頂点バッファと頂点インデックスバッファ
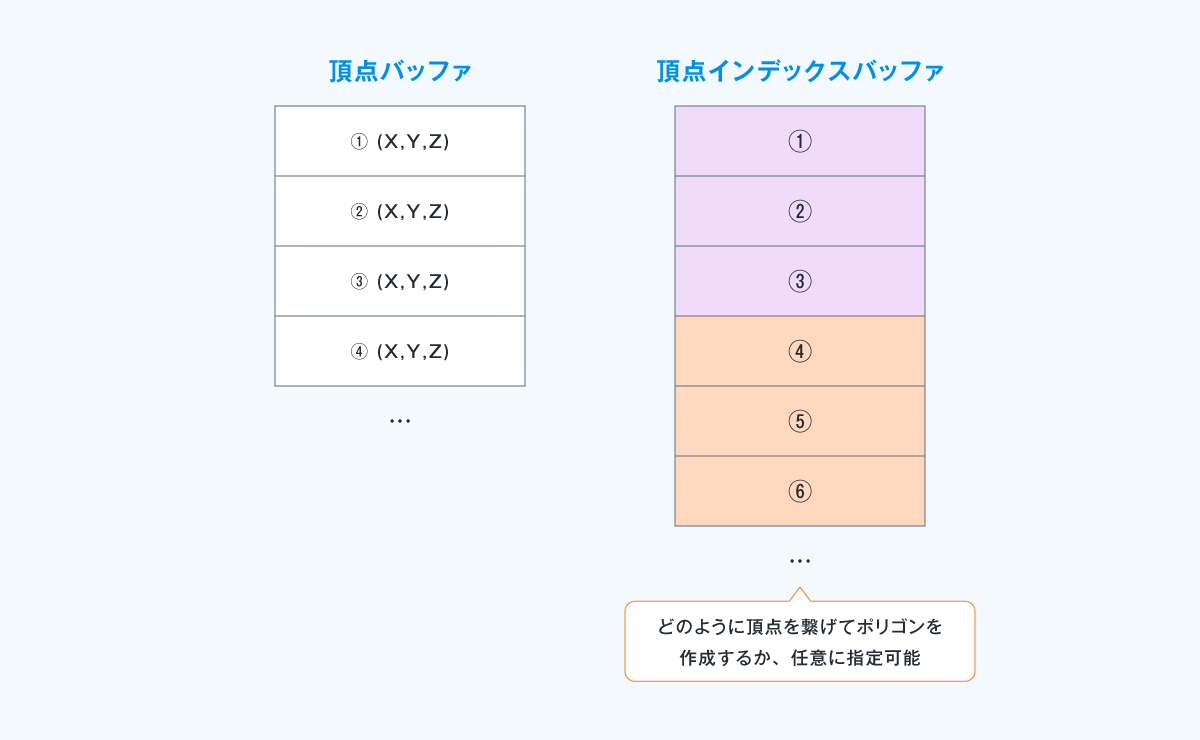
実際に3D描画エンジンでポリゴンを描画する際には、これらの情報を頂点バッファと頂点インデックスバッファに格納して渡します。
“頂点バッファ”は、頂点の座標(X, Y, Z)を格納するための領域です。
“頂点インデックスバッファ”は、頂点バッファ内のどの頂点を使用してポリゴンを描画するかを示す、インデックスを格納するための領域です。
あとは、残りの5つの面についても、同様に頂点インデックスを指定していくことで立方体の描画が実現できます。今回の例ではトータルで頂点バッファは8個、頂点インデックスは12ポリゴン分(36個)の指定が必要になります。
ここで手前の面の1つの正方形を作るのに、①と③の頂点を2回指定していることに注目してください。頂点情報が多くなればなるほど描画処理は重くなるので、重複した頂点を指定するのはできれば避けたいところです。
これについては、3D描画エンジン側に「頂点をどのように結んでポリゴンを作るか」を指定する仕組みが設けられており、複数の三角形ポリゴンを少ない頂点数で、まとめて描画することもできるようになっています。
この仕組みをプリミティブトポロジーと言います。



今回の例ではトライアングルリストが指定されている前提で説明したので1つの正方形を描画するのに頂点インデックスを6個指定しましたが、トライアングルストリップを用いれば、前の三角形を描画するのに使用した頂点の一部を再利用することができる為、1つの正方形を描画するのに指定する頂点インデックスは、①②③④の4個で済みます。
こうすることでデータ量が減らせるというメリットがあります。一方で、指定の方法がややこしく感覚的にわかりにくいので、複雑な形状のモデルを自前で作るのは難しくなります。
「ポリゴンと頂点インデックス」に関する説明は以上となります。


